Dr. Li Yong Lung of the National University of Singapore was invited to give an online lecture on the topic "Second-order Asymptotics of Sequential Hypothesis Testing" in the morning of October 21st, 2022. The report was hosted by Zhou Lin, a teacher from the School of Cyberspace Security of Beihang University. More than 20 teachers and students participated in the report online.
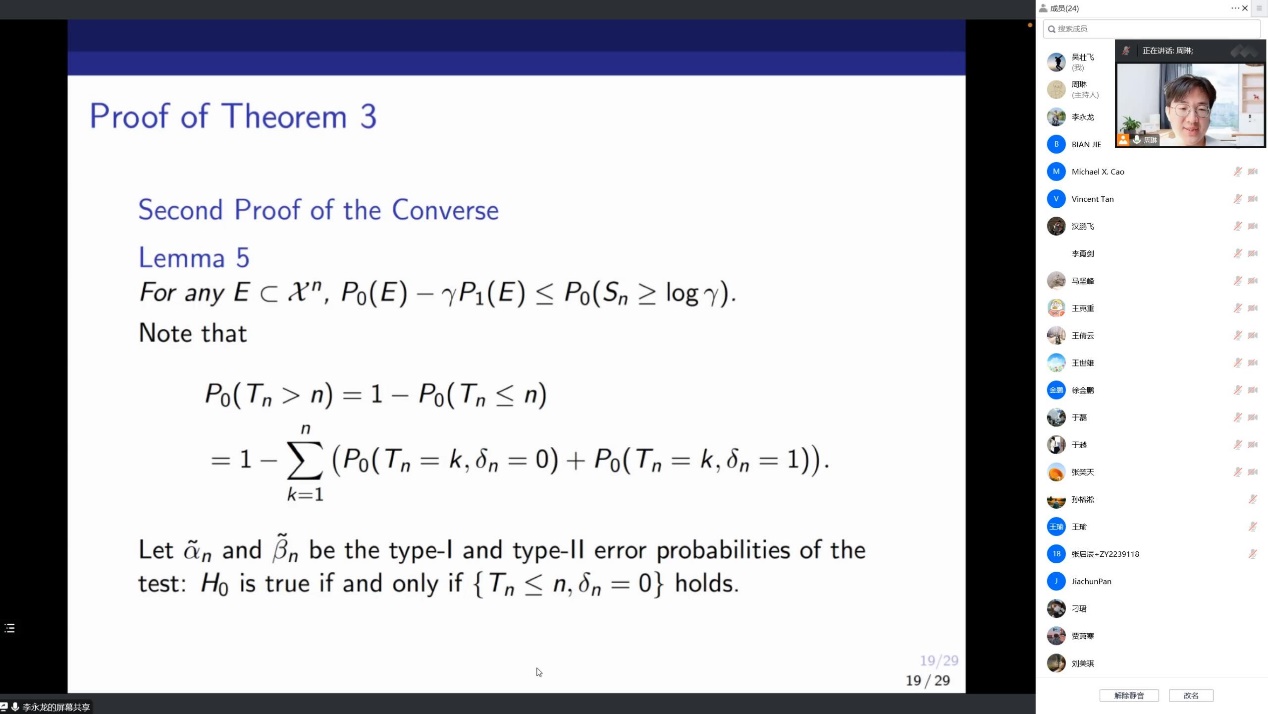
In his report, Dr. Li first introduced the problem of classical sequential binary hypothesis testing, in which there are two hypotheses and the sequence is continuously tested to determine which hypothesis is correct. Dr. Lee then presented classical results in the field, in which Wald and Wolfowitz showed that the optimal error index for type I and type II error probabilities approaches relative entropy as the expectation of test length grows. Dr. Li studied the optimal second-order asymptotic results of this problem by considering two different constraints: test length and sample size. Then, Dr. Li introduced the detailed process of obtaining the above conclusion: First, we consider a probabilistic constraint, in which the probability that the test sequence length exceeds a specified integer n is less than a threshold between 0 and 1. Second, the expected length of the sequence is bounded to n. When some mild conditions are satisfied, the second-order progressiveness of the above cases can be completely described.


In the lecture, Dr. Li Yonglong answered some questions about the system model and mathematical analysis methods. After the lecture, Dr. Li had an in-depth exchange and discussion with the professors and students on the following research direction.
【 Brief Introduction of the Speaker 】
Dr. Li is now a postdoctoral fellow at the National University of Singapore. He graduated from the Department of Mathematics of the University of Hong Kong in 2016, and then did postdoctoral research at the University of California, San Diego and the National University of Singapore. Dr. Li's current research interests include information theory and quantum information theory.